Mixtures and Partial Pressure of Gases with Examples
Mixtures and Partial Pressure of Gases with Example
If gases do not react with each other, they produce homogeneous mixture. Each gas in the container apply pressure. Now we learn concept related to this topic; partial pressure.
Partial Pressure:
Partial pressure of one of the gases in mixture placed in a closed container is equal to pressure of same gas only in same container at same temperature. Following picture summarizes what we try to say.

If temperature and volume of gas are kept constant, partial pressure of gas is directly proportional to number of particles of gas.
Dalton’s Law of Partial Pressure:
“Sum of partial pressures of the gases in the container gives us total pressure of mixture.” This statement is called Dalton’s law of partial pressure. Picture given above also examples of this law.
Ptotal =PH2+PCO2
Gases in same container has equal volumes and they share total pressure according to their number of moles.
If we write ideal gas law for total gas in the mixture and one of the gases and divide them to each other, we get partial pressure equation of one gas in the mixture.
P1.V = n1.R.T
¯¯¯¯ ¯¯¯¯¯¯
Ptotal.V=ntotal.R.T
P1=(n1/ntotal).Ptotal
(n1/ntotal) is called mole fraction of gas1
P2=(n2/ntotal).Ptotal
P3=(n3/ntotal).Ptotal
. . . . . . . . . . . . . . . .
Example: In a closed container, there are 4 gram H2. If we add 4 g He to this container, which ones of the following statements become true? (H=1, He=4)
I. Pressure of H2 is equal to initial pressure of it.
II. Kinetic energies of H2 and He particles are equal in mixture.
III. Partial pressure of H2 in mixture is double of He.
Solution:
I. We find partial pressure of H2, using ideal gas law.
PH2.V=nH2.R.T
PH2=nH2.R.T/V
Since V, T and nH2 are constant, partial pressure of H2 does not change. I is true.
II. Since temperature of homogeneous mixture is same in container, kinetic energies of particles do not change and kinetic energy of H2 particles is equal to kinetic energy of He particles. II is true.
III. Molar mass of H2=2.1=2
Mole of H2;
nH2=4/2=2mol
Mole of He;
nHe=4/4=1mol
Partial pressure is directly proportional to number of moles; Thus partial pressure of H2 is double of partial pressure of He. III is true.
Example: Container contains 0,4mol CH4, 0,1mol SO2, and 0,3mol He. If partial pressure of He is 60cm Hg, which one of the following statement is false? (C=12, H=1, S=32, O=16)
I. Mixture contains 50 % CH4 by mole
II. Total pressure of container is 160 cm Hg
III. Density of SO2 is four times of density of CH4
IV. Partial pressure of SO2 is 20 cm Hg.
Solution:
I. total moles of gases;
ntotal=0,4+0,1+0,3=0,8mol
nCH4=(0,4/0,8).100=50
I is true
II. Partial pressure of He is 60 cm Hg
PHe=(nHe/ntotal).Ptotal
60=(0,3/0,8).Ptotal
Ptotal=160 cm Hg
II is true
III. Molar masses of SO2=32+2.16=64 and CH4=12+4.1=16
masses of mSO2=nSO2.MmSO2=0,1.64=6,4 g and mCH4=nCH4.MmCH4=0,4.16=6,4 g
Since they have equal volumes and masses, d=m/V
their densities are also equal, III is false.
IV. Partial pressure of SO2
PSO2=(nSO2/ntotal).Ptotal
PSO2=(0,1/0,8).160
PSO2=20 cm Hg IV. is true
Pressure of Gases in Combined Containers
Picture given below shows two container combined with tap A.

X and Y gases are put into containers I and II, they are do not react with each other. If we open the tap between containers, which quantities of total system change? We try to answer this question now.
We learned that, gases diffuse from high pressure to low pressure. In this system gas having higher pressure diffuse to other container until pressure balance.Since no reaction occurs initial and final number of moles of X and Y gases are equal. Total number of moles is equal to sum of n1 and n2.
Equation I. ntotal=n1+n2
If we write ideal gas law for each situation;
n1=(P1.V1)/(R.T), n2=(P2.V2/R.T), ntotal=(Pfinal.Vfinal/.RT)
we substitute these equations into equation I. and get;
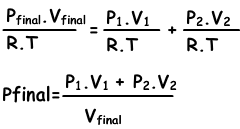
We can write V1+V2 into Vfinal also.
Example: If we open the tap and make system balance, which ones of the following statements become true for this system?

I. Final pressure of Y is larger than initial pressure of Y
II. Partial pressures of X and Y becomes equal.
III. Total pressure becomes 2,4 atm
Solution:
I. Initial volume of gas Y is 6V, final volume of Y is 10 V. Since temperature, number of moles are constant, but volume of Y increases, its pressure decreases. I is false.
II. Partial pressures of gases are directly proportional to their number of moles. We find number of moles of gases and then we give relation betwen their partial pressures using ideal gas law.
n=P.V/R.T
nX=Px.Vx/R.T=3.4V/RT=12V/RT
nY=PY.VY/R.T=2.6V/RT=12V/RT
Since number of moles of gases are equal their partial pressures become also equal.
III. Pfinal=(Px.Vx+Py.Vy)/(Vx+Vy)
Pfinal=(3.4V+2.6V)/(4V+6V)
Pfinal=24V/10V=2,4 atm
III is also true