Gasdichte mit Beispielen
Gasdichte mit Beispielen
Die Dichte der Gase ist in Bezug auf Feststoff- und Gasphasen zu gering. Wir können Dichte mit der folgenden Formel finden;
d (Gas) = m (Gas) / V (Gas)
wenn wir es in das ideale Gasgesetz einsetzen;
P.V = n.R.T wobei n = Masse / Molmasse ist P.V=(m/Mm).R.T
P.Mm=(m/V).R.T
P.Mm=d.R.T
d=(P.Mm)/(R.T)
Wie Sie aus der Formel ersehen können; Die Dichte der Gase ist direkt proportional zu Druck und Molmasse und umgekehrt proportional zur Temperatur.
Beispiel: Bestimmen Sie die Dichte von C4H8 bei 273 0C und einem Druck von 2 atm. (H = 1, C = 12)
Lösung: Wir machen zuerst Einheitenkonventionen. T=273+273=546 K
P=2 atm
C4H8=4.12+8.1=56 g/mol
Unter Verwendung der oben angegebenen Formel;
P.Mm=d.R.T
2.56=d.(22,4/273).546
d=2,5 g/L
Beispiel: Wenn wir bei konstanter Temperatur etwas CH4 in den unten angegebenen Behälter geben; Welche der folgenden Aussagen gelten für Gase in diesem Behälter? (He = 4, C = 12, H = 1)

I. Die Dichte der Mischung nimmt zu
II. Lautstärke erhöht sich
III. Druck steigt an
Lösung:
Molmasse von CH4 = 12 + 4,1 = 16
Da der Kolben des Behälters dynamisch ist, nimmt das Gemischvolumen zu, wenn wir CH4 hinzufügen. Die Molmasse von CH4 ist größer als He, daher nimmt auch die Dichte des Gemisches zu.
PM = d.R.T.
Erhöht sich das Volumen des Gasausgleichsdrucks und bleibt es konstant.
Beispiel: Welche der Grafiken gelten für ideales Gas? 
Lösung: I. Verwendung des idealen Gasgesetzes; P.V=n.R.T
P=n.R.T/V
Da R, n und V konstant sind, ist P direkt proportional zur Temperatur. Grafik I ist wahr.
II. Das Molvolumen beträgt V / n. Unter Verwendung des idealen Gasgesetzes; V/n=R.T/P
Da R, P und T konstant sind, muss V / n konstant sein. Somit ist der zweite Graph falsch, die Linie, die die Beziehung zwischen V und n zeigt, muss parallel zu n sein.
III. Wir schreiben ein ideales Gasgesetz für die Dichte; d=P.Mm/R.T
Mm, R und P sind konstant, d ist also umgekehrt proportional zu T. III. Grafik ist wahr.
Beispiel: Die nachstehende Grafik zeigt die Dichte-Volumen-Beziehung von X (Gas) bei 00 ° C. Wenn der Druck von X (Gas) am Punkt A 1 atm beträgt, welche der folgenden Aussagen gelten für dieses Gas.

I. n=1 Mol
II. Der Druck am Punkt B beträgt 0,5 atm
III. Die Molmasse des Gases beträgt 56 g
Lösung:
I. Ideales Gasgesetz bei Punkt A; PA.VA=n.R.T
T=0 0C or 273 K
V=11,2 Liters
P=1 atm
n=PA.VA/R.T=(1.11,2)/(22,4/273).273)=0,5mol
I. ist falsch.
II. n und T sind konstant, also können wir schreiben; PA.VA=PB.VB
(1.11,2)=PB.22,4
PB=0,5 atm, II ist wahr.
III. Dichte am Punkt A ist;
dA=PA.Mm/R.T
Mm=(dA.R.T)/PA=(2,5.(22,4/273).273)/1
Mm=56 g/mol
1 Mol Gas enthält 56 g, also ist III wahr.
Beispiel: Welche der folgenden Aussagen gelten für He- und O2-Gase bei gleicher Temperatur? (He = 4, O = 16) 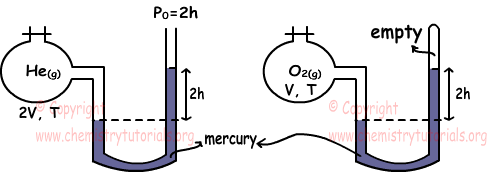
I. nHe=4nO2
II. dHe=8dO2
III. Die durchschnittlichen kinetischen Energien von He und O2 sind gleich.
Lösung:
Mit Manometern ermitteln wir den Gasdruck. PHe=2h+2h=4h
PO2=2h
Um die Beziehung zwischen der Anzahl der Mol Gase zu finden, verwenden wir das ideale Gasgesetz.
PHe.VHe=nHe.R.THe
nHe=4h.2V/R.T
PO2.VO2=nO2.R.TO2
nO2=2h.V/R.T
Ratio of nHe und nO2
nHe/nO2=4/1 Somit, I ist wahr.
Wir finden die Dichte der Gase nach dem idealen Gasgesetz wieder.
Molmasse von He = 4 und Molmasse von O2=2.16=32 dHe=PHe.MHe/R.T
dHe=4h.4/R.T
dO2=PO2.MO2/R.T
dO2=2h.32/R.T
Verhältnis der Dichten;
dHe/d/O2=1/4 , II ist also falsch.
III. Da die Temperatur der Gase gleich ist, sind auch ihre durchschnittlichen kinetischen Energien gleich. III ist wahr.