Ley del Gas Ideal con ejemplos

Ley del Gas Ideal

n de gas ideal, las moléculas no tienen volumen y no hay interacción entre ellos. En términos reales, no hay un gas, es sólo una suposición. Todos los gases reales se ha de pequeños volúmenes y hay interacciones entre ellos. En solución de problemas; asumimos todos los gases como el gas ideal. Ecuación dada a continuación es la ley del gas ideal. Lo conseguimos mediante la combinación de todas las leyes de los gases en la sección anterior.

P.V=n.R.T

Donde, P presión, volumen V , n el número de partículas, R constante de los gases 0,08206 L atm / mol K o 22,4 / 273 L atm / mol K, y T la temperatura

Ahora que resolver algunos problemas relacionados con la ley del gas ideal para una mejor comprensión, se suceden ejemplo atentamente.

Ejemplo: Buscar la presión de 8,8 g de CO₂ a 27 ⁰C en un recipiente con volumen 1230 cm³. (C = 12, O = 16)

Solución: En primer lugar, encontrar la masa molar de CO₂;

CO₂=12+2.16=44

Entonces, nos encontramos con moles de CO₂;

n = 8,8 / 44 = 0,2 moles

Convertir la temperatura de 0 ° C a K y el volumen de cm³ a litro;

T=27+273=300 K

V=1230 cm³=1,23 litros

Ahora, usamos la ley del gas ideal para encontrar la cantidad desconocida.
P.V=n.R.T

P.1,23=0,2.0,08206.300

P=4 atm

Ejemplo: Encontrar la masa molar de X (gas) que figura en el cuadro de abajo con 896 cm³ de volumen, temperatura de 273 °C y la masa de 0,96 g. (O = 16, y la presión atmosférica es de 1 atm)

solución:

Hacemos conversiones de unidades en primer lugar.

P=38 cm Hg=38/76=0,5 atm

V=896/1000=0,896 litros

T=273 + 273=546 K

Ahora, usamos la ley del gas ideal para encontrar n;

P.V=n.R.T

0,5.0,896=n.(22,4/273).546

n=0,03 moles

La masa molar de X;

M_X=m_X/n=0,96/0,03

M_X=32 g/mol

Así ; X(gas)=O₂

Ejemplo: Sistema A continuación se coloca en un lugar con 70 cm de Hg de presión atmosférica. Recipiente con 2 g Él al principio, luego se añade 1 g de gas H₂ a este contenedor. Encontrar la salida del mercurio en el manómetro después de agregar H₂. (He = 4, H₂ = 2)

P_inicial=P₀-20=70-20=50 cm Hg

n_inicial=2/4=0,5mol He

n_H2=1/2=0,5mol H₂

n_final=n_He+n_H2

n_final=0,5+0,5=1mol

Escribimos ley del gas ideal de los valores inicial y final, luego los de buceo entre sí para encontrar el valor desconocido.

V y T son constantes en ambas situaciones.

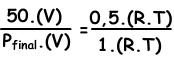
P_final=100 cm Hg

Diferencia entre los niveles de mercurio entre las dos ramas del manómetro;

100-70 = 30 cm en la rama derecha del manómetro

Así la diferencia entre los niveles inicial y final de Hg se convierte;

20 +30 = 50 cm

Este cambio es compartida por dos ramas del manómetro;

50 / 2 = 25 cm

Por lo tanto, se eleva 25 cm Hg en una rama de manómetro.

Gases los exámenes y soluciones a los problemas