Dichtheid Van Gassen Met Voorbeelden
Dichtheid Van Gassen Met Voorbeelden
De dichtheid van gassen is te klein met betrekking tot vaste en gasfasen. We kunnen dichtheid vinden met de volgende formule;
d (gas) = m (gas) / V (gas)
als we het vervangen door de ideale gaswet;
P.V = n.R.T waarbij n = massa / molaire massa
P.V=(m/Mm).R.T
P.Mm=(m/V).R.T
P.Mm=d.R.T
d=(P.Mm)/(R.T)
Zoals u kunt zien in de formule; dichtheid van gassen is recht evenredig met druk en molaire massa en omgekeerd evenredig met temperatuur.
Voorbeeld: vind de dichtheid van C4H8 bij 273 0C en onder een druk van 2 atm. (H = 1, C = 12)
Oplossing: we maken eerst unitconventies; T=273+273=546 K
P=2 atm
C4H8=4.12+8.1=56 g/mol
Gebruik de hierboven gegeven formule;
P.Mm=d.R.T
2.56=d.(22,4/273).546
d=2,5 g/L
Voorbeeld: Als we wat CH4 toevoegen aan de hieronder gegeven container bij constante temperatuur; welke van de volgende uitspraken zijn waar gerelateerd aan gassen in deze container? (He = 4, C = 12, H = 1)

I. De dichtheid van het mengsel neemt toe
II. Volume neemt toe
III. Druk stijgt
Oplossing:
Molaire massa van CH4 = 12 + 4,1 = 16
Omdat de zuiger van de container dynamisch is, neemt het volume van het mengsel toe wanneer we CH4 toevoegen. Molaire massa van CH4 is groter dan He, dus de dichtheid van het mengsel neemt ook toe.
P.Mm = d.R.T
Het volume van de gasbalansdruk neemt toe en het blijft constant.
Voorbeeld: Welke van de grafieken kloppen voor ideaal gas. 
Oplossing:
I. Gebruik van de ideale gaswet;
P.V = n.R.T
P = n.R.T / V
Omdat R, n en V constant zijn, is P direct evenredig met de temperatuur. Grafiek I is waar.
II. Molair volume is V / n. Met behulp van ideale gaswetgeving;
V / n = R.T. / P
Omdat R, P en T constant zijn, moet V / n constant zijn. De tweede grafiek is dus onwaar, de lijn die de relatie tussen V en n toont, moet parallel zijn aan n.
III. We schrijven ideale gaswet voor dichtheid; d=P.Mm/R.T
Mm, R en P zijn constant, dus is d omgekeerd evenredig met T. III. grafiek is waar.
Voorbeeld: Onderstaande grafiek toont de dichtheid versus volume-relatie van X (gas) bij 00C. Als de druk van X (gas) op punt A 1 atm is, welke van de volgende beweringen gelden dan voor dit gas. 
I. n = 1 mol
II. Druk op punt B is 0,5 atm
III. Molaire massa gas is 56 g
Oplossing:
I.
Ideale gaswet op punt A; PA.VA=n.R.T
T=0 0C or 273 K
V=11,2 Liters
P=1 atm
n=PA.VA/R.T=(1.11,2)/(22,4/273).273)=0,5mol
I is fout.
II. n en T zijn constant, dus kunnen we schrijven;
PA.VA=PB.VB
(1.11,2)=PB.22,4
PB=0,5 atm, II is waar
III. dichtheid op punt A is;
dA=PA.Mm/R.T
Mm=(dA.R.T)/PA=(2,5.(22,4/273).273)/1
Mm=56 g/mol
1 mol gas bevat 56 g, dus III is waar.
Voorbeeld: Welke van de volgende beweringen zijn waar voor He en O2 gassen onder dezelfde temperatuur. (Hij = 4, O = 16) 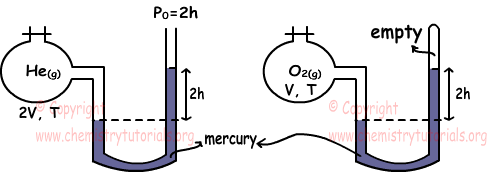
I. nHe=4nO2
II. dHe=8dO2
III. Gemiddelde kinetische energieën van He en O2 zijn gelijk.
Oplossing:
We vinden druk van gassen met behulp van manometers. PHe=2h+2h=4h
PO2=2h
Om de relatie tussen het aantal mol gassen te vinden, gebruiken we de ideale gaswet.
PHe.VHe=nHe.R.THe
nHe=4h.2V/R.T
PO2.VO2=nO2.R.TO2
nO2=2h.V/R.T
Verhouding van nHe en nO2
nHe/nO2=4/1 Dus ik ben waar.
We vinden de dichtheid van gassen opnieuw met behulp van de ideale gaswet.
Molaire massa van He = 4 en Molaire massa van
O2 = 2,16 = 32 dHe=PHe.MHe/R.T
dHe=4h.4/R.T
dO2=PO2.MO2/R.T
dO2=2h.32/R.T
Ratio de las densidades; dHe/d/O2=1/4 dus II is onwaar.
III. Omdat de temperatuur van gassen hetzelfde is, zijn hun gemiddelde kinetische energieën ook hetzelfde. III is waar.