Ideale Gas Wet
Ideale Gaswet
Een ideaal gas; moleculen hebben geen volume en er is geen interactie tussen hen. In het echt bestaat zo’n gas niet, het is slechts een veronderstelling. Alle echte gassen hebben kleine volumes en er zijn interacties tussen hen. In probleemoplossingen; we nemen alle gassen aan als ideaal gas. De onderstaande vergelijking is de ideale gaswet. We krijgen het door alle gaswetten te combineren die in de laatste sectie zijn gegeven.
P.V=n.R.T
Waar; P druk, V volume, n aantal deeltjes, R gasconstante 0,08206 L atm / K mol of 22,4 / 273 L atm / K mol, en T temperatuur
Nu lossen we enkele problemen op met betrekking tot de ideale gaswet voor een beter begrip, volg elk voorbeeld zorgvuldig.
Voorbeeld: vind een druk van 8,8 g CO2 bij 27 ° C in een container met een volume van 1230 cm3. (C = 12, O = 16)
Oplossing: we vinden eerst een molaire massa CO2;
CO2=12+2.16=44
Dan vinden we mollen van CO2;
n=8,8/44=0,2 mol
Het omzetten van temperatuur van ° C naar K en volume van cm3 naar liter;
T=27+273=300 K
V=1230 cm3=1,23 liters
Nu gebruiken we de ideale gaswet om een onbekende hoeveelheid te vinden.
P.V=n.R.T
P.1,23=0,2.0,08206.300
P=4 atm
Voorbeeld: Vind de molmassa van X (gas) weergegeven in de onderstaande afbeelding met volume 896 cm3 temperatuur 273 ° C en massa 0,96g. (O = 16 en atmosferische druk is 1 atm)

Oplossing:
We maken eerst eenheidsconversies. P=38 cm Hg=38/76=0,5 atm
V=896/1000=0,896 liters
T=273 + 273=546 K
Nu gebruiken we de ideale gaswet om n te vinden;
P.V=n.R.T
0,5.0,896=n.(22,4/273).546
n=0,03 mol
Molaire massa van X;
MX=mX/n=0,96/0,03
MX=32 g/mol
Dus; X(gas)=O2
Voorbeeld: Onderstaand systeem wordt geplaatst op een locatie met een atmosferische druk van 70 cm Hg. Container heeft eerst 2 g He, daarna voegen we 1 g H2 gas toe aan deze container. Zoek de stijging van Hg in de manometer na toevoeging van H2. ( He=4, H2=2)

Peerste=P0-20=70-20=50 cm Hg
neerste=2/4=0,5mol He
nH2=1/2=0,5mol H2
nlaatste=nHe+nH2
nlaatste=0,5+0,5=1mol
We schrijven ideale gaswet voor begin- en eindwaarden, waarna we ze naar elkaar duiken om een onbekende waarde te vinden.
V en T zijn constant in twee situaties. 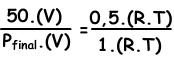
Plaatste=100 cm Hg
Verschil tussen Hg-niveaus tussen twee takken van de manometer;
100-70 = 30 cm in rechter tak van manometer
Aldus wordt verschil tussen begin- en eindwaarden van Hg;
20 + 30 = 50 cm
Deze wijziging wordt gedeeld door twee takken van manometer;
50/2 = 25 cm
Aldus stijgt Hg 25 cm in een tak van de manometer.