Mengsels En Partiële Druk Van Gassen Met Voorbeeld
Mengsels En Partiële Druk Van Gassen Met Voorbeeld
Als gassen niet met elkaar reageren, produceren ze een homogeen mengsel. Elk gas in de container oefent druk uit. Nu leren we concept gerelateerd aan dit onderwerp; gedeeltelijke druk.
Gedeeltelijke Druk:
De partiële druk van een van de gassen in een mengsel geplaatst in een gesloten container is gelijk aan de druk van hetzelfde gas alleen in dezelfde container bij dezelfde temperatuur. De volgende foto vat samen wat we proberen te zeggen. 
Als de temperatuur en het volume van het gas constant worden gehouden, is de partiële gasdruk recht evenredig met het aantal gasdeeltjes.
Dalton’s Wet Van Gedeeltelijke Druk: “Som van gedeeltelijke drukken van de gassen in de container geeft ons totale mengdruk.” Deze verklaring wordt de wet van Dalton van gedeeltelijke druk genoemd. Afbeelding hierboven ook voorbeelden van deze wet.
Ptotal =PH2+PCO2
Gassen in dezelfde container hebben gelijke volumes en ze delen de totale druk op basis van hun aantal mol.
Als we de ideale gaswet schrijven voor totaal gas in het mengsel en een van de gassen en deze onderling verdelen, krijgen we een partiële drukvergelijking van één gas in het mengsel.
P1.V = n1.R.T
Ptotal.V=ntotal.R.T
P1=(n1/ntotal).Ptotal
(n1/ntotal) wordt molfractie van gas1 genoemd
P2=(n2/ntotal).Ptotal
P3=(n3/ntotal).Ptotal
Voorbeeld: In een gesloten container zit 4 gram H2. Als we 4 g Hij aan deze container toevoegen, welke van de volgende beweringen worden dan waar? (H = 1, He = 4)
I. De druk van H2 is gelijk aan de initiële druk ervan.
II. Kinetische energieën van H2 en He-deeltjes zijn gelijk in mengsel.
III. De partiële druk van V in mengsel is het dubbele van He.
Oplossing:
I. We vinden gedeeltelijke druk van H2, met behulp van ideale gaswetgeving.
PH2.V=nH2.R.T
PH2=nH2.R.T/V
Omdat V, T en nH2 constant zijn, verandert de partiële H2 druk niet. Ik ben waar.
II. Omdat de temperatuur van het homogene mengsel hetzelfde is in de container, veranderen de kinetische energieën van deeltjes niet en is de kinetische energie van H2 deeltjes gelijk aan kinetische energie van He deeltjes. II is waar.
III. Molaire massa van H2 = 2,1 = 2
Mol H2; nH2=4/2=2mol
Mol He;
nHe=4/4=1mol
Gedeeltelijke druk is recht evenredig met het aantal mol; De partiële druk van H2 is dus het dubbele van de partiële druk van He. III is waar.
Voorbeeld: Container bevat 0,4 mol CH4, 0,1 mol SO2 en 0,3 mol He. Als de gedeeltelijke druk van Hij 60 cm Hg is, welke van de volgende bewering is dan niet waar? (C = 12, H = 1, S = 32, O = 16)
I. Het mengsel bevat 50% CH4 per mol
II. De totale druk van de container is 160 cm Hg
III. De dichtheid van SO2 is vier keer de dichtheid van CH4
IV. De partiële druk van SO2 is 20 cm Hg.
Oplossing:
I. totaal aantal mol gassen;
ntotal=0,4+0,1+0,3=0,8mol
nCH4=(0,4/0,8).100=50
I is waar.
II. Gedeeltelijke druk van Hij is 60 cm Hg
PHe=(nHe/ntotal).Ptotal
60=(0,3/0,8).Ptotal
Ptotal=160 cm Hg
II is waar.
III. Molaire massa van
SO2=32+2.16=64 en CH4=12+4.1=16
massa van mSO2=nSO2.MmSO2=0,1.64=6,4 g en mCH4=nCH4.MmCH4=0,4.16=6,4 g
Omdat ze gelijke volumes en massa’s hebben, d = m / V
hun dichtheden zijn ook gelijk, III is vals.
IV. Gedeeltelijke druk van
SO2 PSO2=(nSO2/ntotal).Ptotal
PSO2=(0,1/0,8).160
PSO2=20 cm Hg IV. is waar.
Druk Van Gassen In Gecombineerde Containers
De onderstaande afbeelding toont twee containers gecombineerd met kraan A.
 X en Y gassen worden in containers I en II geplaatst, ze reageren niet met elkaar. Als we de kraan tussen containers openen, welke hoeveelheden van het totale systeem veranderen? We proberen deze vraag nu te beantwoorden. We hebben geleerd dat gassen diffunderen van hoge druk naar lage druk. In dit systeem diffundeert gas met een hogere druk naar een andere houder tot de drukbalans. Aangezien er geen reactie optreedt, zijn het initiële en uiteindelijke aantal mol X en Y gassen gelijk. Totaal aantal mol is gelijk aan som van
X en Y gassen worden in containers I en II geplaatst, ze reageren niet met elkaar. Als we de kraan tussen containers openen, welke hoeveelheden van het totale systeem veranderen? We proberen deze vraag nu te beantwoorden. We hebben geleerd dat gassen diffunderen van hoge druk naar lage druk. In dit systeem diffundeert gas met een hogere druk naar een andere houder tot de drukbalans. Aangezien er geen reactie optreedt, zijn het initiële en uiteindelijke aantal mol X en Y gassen gelijk. Totaal aantal mol is gelijk aan som van
n1 en n2.
Vergelijking I
ntotal=n1+n2 Als we voor elke situatie een ideale gaswet schrijven;
n1=(P1.V1)/(R.T), n2=(P2.V2/R.T), ntotal=(Pfinal.Vfinal/.RT)
we vervangen deze vergelijkingen in vergelijking I. en krijgen;
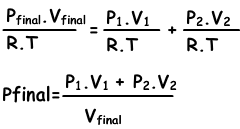
We kunnen ook V1 + V2 into Vfinal schrijven.
Voorbeeld: Als we de kraan openen en het systeem in balans brengen, welke van de volgende beweringen worden dan waar voor dit systeem? 
I. Einddruk van Y is groter dan aanvankelijke druk van Y
II. Gedeeltelijke drukken van X en Y worden gelijk.
III. Totale druk wordt 2,4 atm
Oplossing:
I. Het beginvolume van gas Y is 6V, het eindvolume van Y is 10 V. Aangezien de temperatuur het aantal mol constant is, maar het volume van Y toeneemt, neemt de druk af. I is fout.
II. Gedeeltelijke drukken van gassen zijn recht evenredig met hun aantal mol. We vinden het aantal mol gassen en geven vervolgens een relatie tussen hun partiële druk met behulp van de ideale gaswet.
n=P.V/R.T
nX=Px.Vx/R.T=3.4V/RT=12V/RT
nY=PY.VY/R.T=2.6V/RT=12V/RT
Omdat het aantal mol gassen gelijk is, wordt ook hun partiële druk gelijk.
III. Pfinal=(Px.Vx+Py.Vy)/(Vx+Vy)
Pfinal=(3.4V+2.6V)/(4V+6V)
Pfinal=24V/10V=2,4 atm
III is waar.