Fasen (Staten) Van Materie Met Voorbeelden

Fasen (Staten) Van Materie Met Voorbeelden

Zaken kunnen in vier staten bestaan; vast, vloeibaar, gas en plasma. Enkele specifieke eigenschappen van deze fasen worden in de onderstaande tabel gegeven.

In deze eenheid zullen we vaste stoffen, vloeistoffen en gassen onderzoeken. De onderstaande vorm geeft een samenvatting van de faseveranderingen van zaken van vast naar vloeibaar, van vloeibaar naar gas.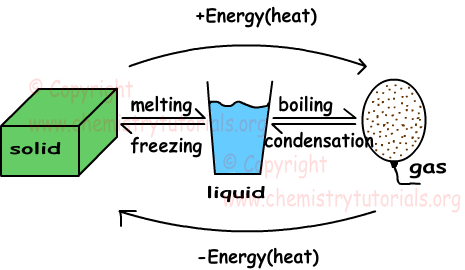

Het verkrijgen van warmte in drie fasen van materie verhoogt de gemiddelde kinetische energieën van deeltjes. Overigens is de kinetische energie van deeltjes in de gasfase groter dan de kinetische energieën in vaste en vloeibare toestand. Definities van enkele concepten met betrekking tot faseverandering worden hieronder gegeven.

Smelten: vaste stof verandert van toestand in vloeistof.

Invriezen: Het tegenovergestelde smeltproces wordt bevriezen genoemd. Vloeibare materie verliest warmte en verandert van toestand naar vast.

Koken: vloeibare stoffen winnen warmte en veranderen hun toestand in gas.

Condensatie: Het tegenovergestelde kookproces wordt condensatie genoemd. Gasmoleculen verliezen warmte en veranderen de fase ervan in vloeistof.

Tijdens faseverandering blijft de temperatuur van zaken constant. Grafieken van faseverandering worden hieronder gegeven.

Temperatuur versus tijd grafiek van verwarmde zuivere vaste stof wordt hieronder gegeven.

In intervallen I. III. en V. temperatuur van materie neemt toe. Omdat materie zuiver is, neemt de kinetische energie ervan ook toe. We kunnen de verkregen warmte vinden in deze intervallen met de volgende formule;

Q=m.c.ΔT

waar; m is massa, c is specifieke warmtecapaciteit en ΔT is verandering in de temperatuur (Tlaatste - Tinitiaal)

In intervallen II. en IV. temperatuur van materie blijft constant omdat materie van fase verandert. Omdat de temperatuur van materie constant is, is de kinetische energie ervan ook constant. Integendeel, tijdens faseverandering nemen afstanden tussen moleculen toe, dus neemt de potentiële energie van materie ook toe. In deze intervallen hebben we heterogene mengsels, bijvoorbeeld in interval II. we hebben een vast + vloeibaar mengsel en in interval IV. we hebben vloeistof + gasmengsel. We vinden de benodigde warmte in deze intervallen met de volgende formules; Q=m.L_fusie or Q=m.L_verdamping

waarbij, m massa is, LFusion latente smeltwarmte is en Verdamping latente verdampingswarmte is.
Het verliezen van warmte van materie in gasfase heeft een temperatuur versus tijd grafiek zoals hieronder gegeven.

Zoals u in beide grafieken kunt zien, wordt het kookpunt condensatiepunt en smeltpunt wordt het vriespunt in het koelproces. Hun grootte is gelijk. We gebruiken dezelfde formules die hierboven zijn gegeven om tijdens dit proces vrijkomende warmte te vinden.

We lossen enkele voorbeelden op met betrekking tot faseverandering.

Voorbeeld: Vind de benodigde warmte om de temperatuur van 100 g ijs te verhogen van 0⁰C tot 40 ° C.(c_water=1cal/g⁰C, L_fusie=80cal/g)

Oplossing:

We smelten eerst ijs en verwarmen het vervolgens tot 40 ° C.

Q₁=m.Lfusie

Q₁=100g.80.cal/g

Q₁=8000 cal

Nu verhogen we de temperatuur van 0 tot 40⁰C

Q₂=m.c.ΔT

Q₂=100.1.(40-0)

Q₂=4000cal

Q_totaal=Q₁+Q₂=8000cal+4000cal=12000cal.

Voorbeeld: Als we twee wateren mengen met een massa van 150 g, temperatuur 40 ⁰C en 100 g en 80 ⁰C, zoek dan de eindtemperatuur van mengsels.(cwater=1cal/g.⁰C)

Oplossing:

Wanneer twee zaken met verschillende temperaturen met elkaar in contact zijn, is er een warmteoverdracht tussen hen. Warmte stroomt van materie met hogere temperatuur naar materie met lage temperatuur totdat ze gelijke temperaturen hebben. Opgewekte warmte is altijd gelijk aan verloren warmte.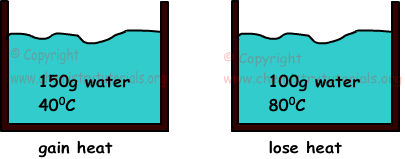

temperatuur van het uiteindelijke mengsel moet tussen de temperaturen van beide wateren liggen

40⁰C<T_laatste<80⁰C

Q_opgedaan=Q_verloren

m₁.c₁. ΔT₁=m₂.c₂.ΔT₂

150.1.(T-40)=100.1.(80-T)

T=56⁰C

Materie En Eigenschappen Van Materie Examens En Probleem Oplossingen